pythonで時間周波数解析~STFT~

時間周波数解析(Time–frequency analysis)とは、音などの信号を時間軸と周波数軸に分解する解析手法のことです。
また、その結果を表示したグラフをスペクトログラムと呼びます。
時間周波数解析の手法は大きく分けて3つあります。
それぞれの特徴を下に示します。

	時間分解能	周波数分解能	特徴	pythonライブラリ
STFT	トレードオフの関係		安定・簡単・大雑把	scipy.signal.stft matplotlib.pyplot.specgram
ウェーブレット変換	高周波:高い低周波:低い	高周波:低い低周波:高い	分解能が周波数依存	scipy.signal.cwt pywt.cwt
ウィグナー分布	高い	高い	交差項(偽像)が生じる	tftb.processing (PDFドキュメント)

今回は一番簡単なSTFTを実際に使ってみて、パラメータの説明などをします。

音源はESC-50というデータセットからお借りしました。

データセットのリポジトリはこちら➡https://github.com/karolpiczak/ESC-50

siren(サイレン)のタグがついたファイルを借りました➡1-76831-A-42.wav

matplotlibを用いたSTFT

まずはより簡単なmatplotlibを用いたSTFTをしてみます。
ここにあるようにしてwavファイルを読み込みます。
matplotlibは変換と同時にプロットしてくれます。

if __name__ == "__main__":
    wave, fs = wav_read(path_to_wavfile)
    Pxx, freqs, bins, im = plt.specgram(wave, Fs=fs, cmap = 'jet', mode='magnitude')
    x1, x2, y1, y2 = plt.axis()
    plt.axis((x1, x2, y1, y2))
    plt.show()
    plt.close()

実行結果はこんな感じです。

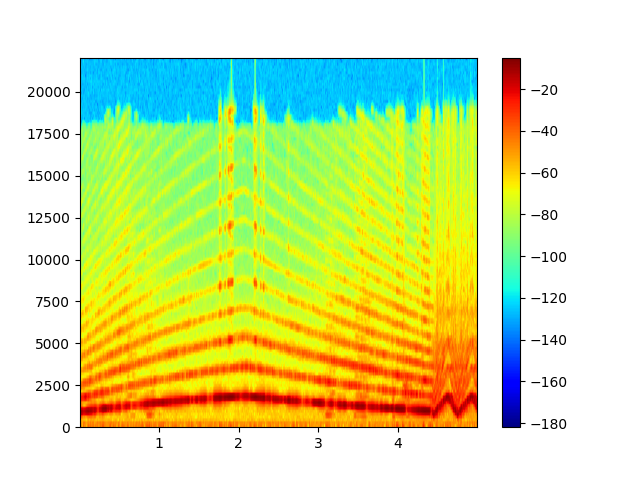
それっぽく見えます。

scipyを用いたSTFT

matplotlibを使ってSTFTをしてると音データが大きい時にMemoryErrorが吐かれてしまうことがありました。
内部処理は分かりませんが、scipyだとMemoryErrorが起きなかったのでscipyを使った方法を紹介します。
引数等はmatplotlibと大差ないです。
グラフのプロットにはmatplotlib.pyplot.pcolormeshを使います。

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal
import math

if __name__ == "__main__":
    wave, fs = wav_read(path_to_wavfile)
    frq, t, Pxx = scipy.signal.stft(wave, fs=fs) #周波数、時間、強さの3つの情報が帰ってくる
    Pxx = 10 * np.log(np.abs(Pxx)) #対数表示に直す
    plt.pcolormesh(t, frq, Pxx, cmap = 'jet')
    plt.show()
    plt.close()

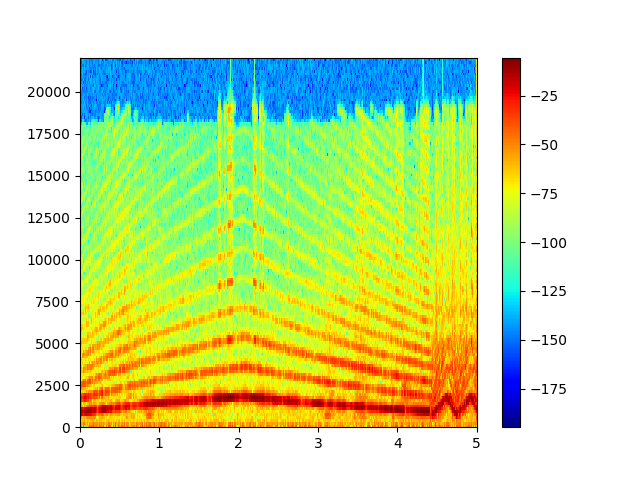
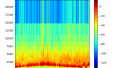
ほとんど同じグラフがプロットできましたね、正しそうです。

原理、引数の軽い説明

短時間フーリエ変換(STFT, short-time Fourier transform)は信号に窓関数をずらしながらかけてフーリエ変換する変換のことです。

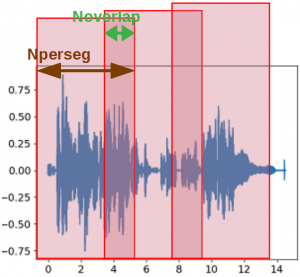
この赤い枠が窓関数に相当していて、上記2つのライブラリでは窓関数の幅(Nperseg(matplotlibではNFFT))と窓関数の重なり(Noverlap)を指定できます。
(実際には窓関数はこの図より細かく設定すると思いますが)
Npersegを大きくするほど窓関数が大きくなり周波数分解能が高くなる。
NoverlapがNpersegより小さい範囲でより大きくしてあげると時間分解能が高くなるように見える。
みたいなイメージを持っていただければよいと思います。