以前、時間周波数解析をSTFTとウェーブレット変換でやりました。 今回は定Q変換(CQT: Constant-Q transform)をやってみます。 定Q変換の特徴として、低周波数で良い分解能を示します。 音色変換等の深層学習の前処理に使われることもあるみたいです。
以前と同様に、音源はESC-50というデータセットからお借りしました。 データセットのリポジトリはこちら➡https://github.com/karolpiczak/ESC-50 siren(サイレン)のタグがついたファイルを借りました➡1-76831-A-42.wav
librosa.cqtを用いた定Q変換
音響信号処理によく使われるライブラリであるlibrosaを用います。 このライブラリはpipでインストールできます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import matplotlib.pyplot as plt import numpy as np import librosa if __name__ == "__main__": bins = 84 hop_length = 512 fmin = 32.7 cqt = librosa.cqt(wave,sr=fs, hop_length=hop_length, fmin=fmin, n_bins=bins) D = librosa.amplitude_to_db(cqt, ref=np.max) #定Q変換 frq = librosa.cqt_frequencies(n_bins=bins,fmin=fmin) #周波数軸 t = librosa.frames_to_time(np.arange(D.shape[1] + 1), sr=fs, hop_length=hop_length) #時間軸 plt.pcolormesh(t, frq, 10 * np.log(np.abs(cqt)), cmap='jet') plt.colorbar() plt.show() plt.close() |
結果は以下のグラフです。低周波数で良い分解能ですね。
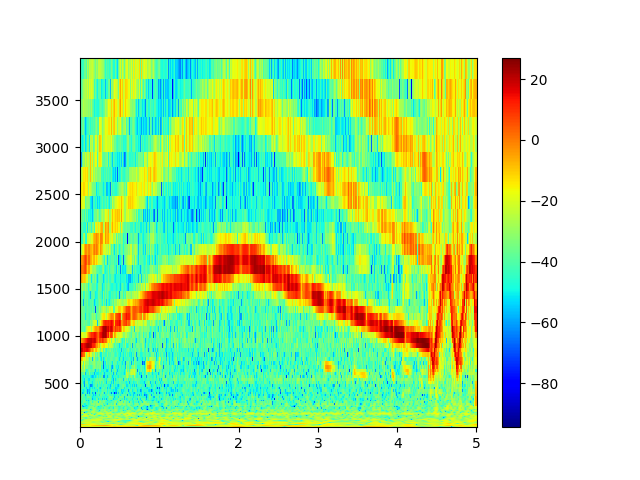
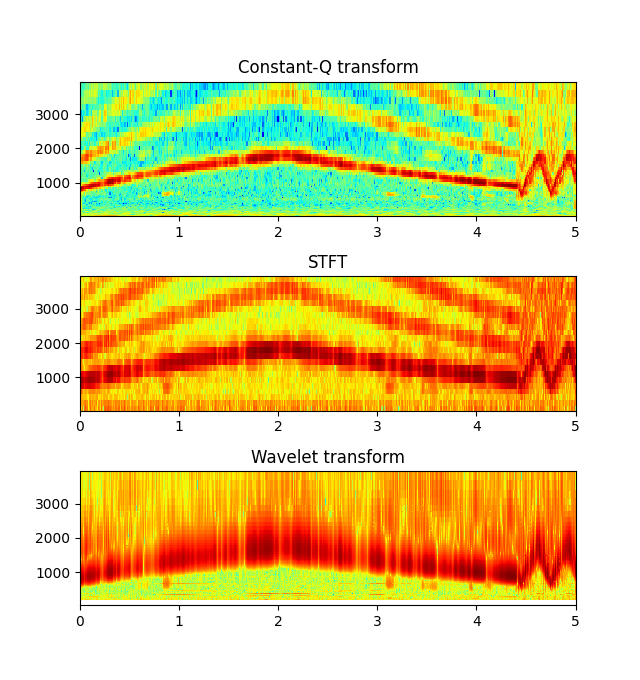
比較のためにSTFT、ウェーブレット変換の結果をプロットしてみます。
確かに定Q変換の結果がきれいな気もします。
コメント