pythonで音量を計算する

pythonによる信号処理です。今回は音声信号から音量波形を求めます。
音声信号の音量の変化を見たい時はたまにあると思います。
計算には二乗平均平方根(RMS: root mean square）を用います。
音声信号をある程度の範囲で区切り、その部分部分でRMSを計算することで音量の変化を見ていきます。

音源はESC-50というデータセットからお借りしました。
データセットのリポジトリはこちら➡https://github.com/karolpiczak/ESC-50
hen(めんどり)のタグがついたファイルを借りました➡1-5996-A-6.wav

librosaを用いた音量計算

librosaの音量を計算する関数librosa.feature.rmsを用います。
rmsの引数を変更することでrmsを求める区間等を変更できます。
今回はデフォルトのままやっています。

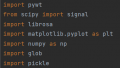
import librosa
import matplotlib.pyplot as plt
if __name__ == "__main__":
    wave, fs = wav_read(path_to_wavefile)
    rms = librosa.feature.rms(y=wave) #音量の計算
    times = librosa.times_like(rms, sr=fs) #時間軸の生成
    plt.plot(times, rms[0]*2**(1/2)) #rms➡振幅に変換
    plt.show()
    plt.close()

結果は下のグラフです。
音量の変化が求められています。

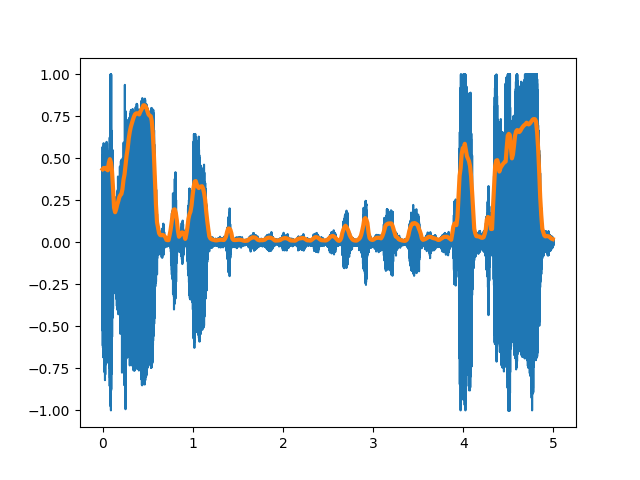
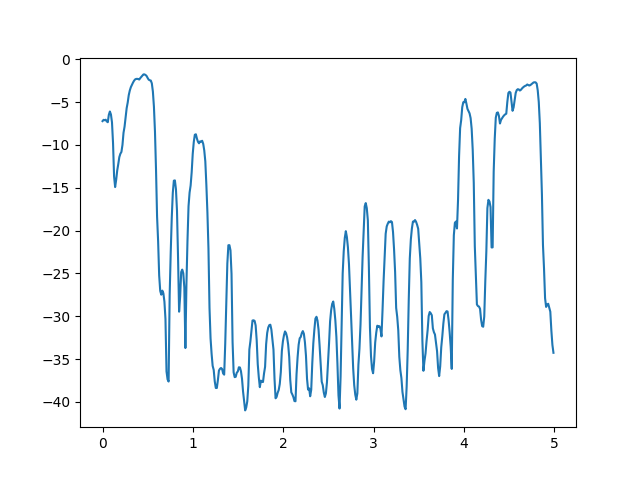
また、人の音量の知覚は振幅の対数に比例するため、デシベルに変換したものもよく用いられます。